线性回归分析是一种重要的统计方法，用于描述自变量与因变量之间的线性关系。它常用于预测、趋势分析和因果推断等领域。在SPSS中，进行线性回归分析可以帮助研究人员发现数据中的规律，并建立有效的预测模型。本文将详细介绍线性回归的基本概念，并为您提供如何使用SPSS进行线性回归建模的详细步骤。

　　1. 线性回归概述

　　线性回归（Linear Regression）是用于分析两个或多个变量之间关系的统计方法。它通过建立一个数学模型，来描述自变量（X）对因变量（Y）的影响。在回归模型中，Y是因变量，X是自变量，线性回归假设自变量和因变量之间存在线性关系。

　　线性回归模型的基本形式为：

　　Y=β0+β1X+ϵ

　　其中：

　　Y 是因变量X是自变量β0是截距（常数项）β1是自变量的回归系数（反映自变量对因变量的影响）ϵ 是误差项，表示其他因素对因变量的影响

　　线性回归模型的目标是估计回归系数 β0\beta_0β0​ 和 β1\beta_1β1​，并通过这些系数来预测因变量的值。

　　2. 如何使用SPSS进行线性回归建模

　　SPSS是一个功能强大的统计分析软件，它提供了简单直观的界面来进行线性回归分析。以下是利用SPSS进行线性回归建模的详细步骤：

　　步骤一：打开数据集

　　首先，确保您已经在SPSS中加载了数据集。数据集应该包含您想要进行回归分析的自变量和因变量。假设您要研究“广告费用”（自变量）对“销售额”（因变量）的影响。

　　步骤二：选择回归分析

　　在SPSS主界面，点击菜单栏中的：

　　分析（Analyze）选择 回归（Regression）然后点击 线性（Linear）。

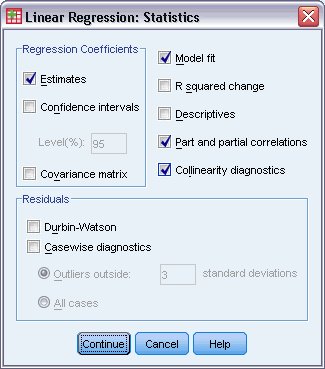
　　步骤三：选择自变量和因变量

　　在弹出的对话框中，您将看到两个主要选项：

　　因变量（Dependent）：将因变量（例如“销售额”）拖动到这个框中。自变量（Independent(s)）：将自变量（例如“广告费用”）拖动到这个框中。

　　步骤四：选择其他设置

　　SPSS提供了多种选项来优化回归分析的结果：

　　方法（Method）：选择回归方法。通常选择“进入”（Enter），这意味着所有自变量将一起进入回归模型。统计量（Statistics）：您可以选择是否查看一些附加统计量，如回归系数、标准误差、R平方值等。残差（Residuals）：选择是否查看回归分析的残差，以便检查模型的拟合情况。

　　步骤五：运行回归分析

　　设置完成后，点击**确定（OK）**按钮，SPSS将执行回归分析，并输出回归分析结果。

　　3. 解读SPSS线性回归分析结果

　　SPSS完成线性回归分析后，您将看到一个详细的输出结果，包括以下几个关键部分：

　　1. 模型摘要（Model Summary）

　　该部分显示了回归模型的总体拟合情况，主要包含：

　　R：表示自变量与因变量之间的相关性。R平方（R²）：表示回归模型能够解释的因变量方差的比例。R²值越大，说明模型拟合效果越好。

　　2. ANOVA表（ANOVA）

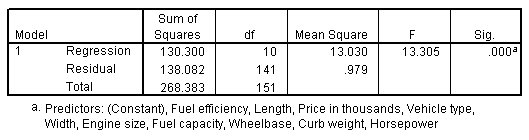
　　ANOVA表用于检验回归模型是否显著。它显示了模型的F统计量及其对应的p值。若p值小于0.05，表示回归模型在统计上显著。

　　3. 回归系数（Coefficients）

　　回归系数表显示了每个自变量的回归系数、标准误差、t值和p值。在这里，您可以看到自变量对因变量的影响程度和显著性。

　　回归系数（B）：表示自变量对因变量的影响程度。如果回归系数为正，说明自变量与因变量呈正相关；如果为负，则为负相关。标准误差（Std. Error）：衡量回归系数估计值的准确度。t值和p值：用于检验回归系数是否显著。如果p值小于0.05，说明该自变量在模型中具有显著影响。

　　4. 残差分析（Residuals）

　　残差分析帮助您评估回归模型的拟合情况。通过残差图，您可以检查模型是否存在非线性关系或异方差性等问题。

　　4. 线性回归模型的实际应用

　　线性回归模型广泛应用于各个领域，尤其在经济学、市场营销、医学研究等领域中具有重要作用。例如：

　　市场营销：分析广告费用与销售额之间的关系，为广告预算分配提供依据。经济学：研究人均收入与消费支出之间的关系，预测经济发展趋势。医学：通过回归分析研究药物剂量与疗效之间的关系，为临床治疗提供参考。

　　5. 总结

　　线性回归分析是一种强大的统计工具，用于探索自变量和因变量之间的线性关系。通过SPSS，您可以快速构建线性回归模型，并评估其准确性和显著性。了解如何使用SPSS进行线性回归分析，对于任何需要进行数据建模和预测分析的研究者来说都是一项必备技能。希望通过本文，您能够掌握SPSS中线性回归分析的基本方法，应用到您的实际研究中。