双因子方差分析（Two-Way ANOVA）是一种常用的统计方法，用于分析两个自变量对一个因变量的影响，并检查这两个自变量是否有交互作用。在SPSS中，双因子方差分析可以通过GLM（广义线性模型）单变量分析来实现。GLM是SPSS中功能强大的工具，适用于多种方差分析任务，包括双因子方差分析。以下是如何使用GLM单变量进行双因子方差分析的详细教程。

　　1. 准备数据

　　在进行双因子方差分析之前，首先需要准备好数据。假设你有两个自变量和一个因变量。自变量通常是分类变量（例如“性别”和“治疗方法”），而因变量是一个连续变量（例如“成绩”或“反应时间”）。例如，你可能想要分析“性别”和“治疗方法”对“成绩”的影响，并检查它们是否存在交互作用。

　　在SPSS中，数据应以每个观测为一行的形式组织，每一列对应一个变量。确保自变量是分类变量（例如，性别可能有“男”和“女”两个水平，治疗方法可能有“药物”和“安慰剂”两个水平），因变量是连续变量。

　　2. 打开GLM单变量分析菜单

　　执行双因子方差分析的步骤如下：

　　在SPSS中，点击分析 > 一般线性模型 > 单变量（Analyze > General Linear Model > Univariate）。弹出窗口后，在“因变量”框中选择你的因变量（例如“成绩”）。在“固定因子”框中，选择你的两个自变量（例如“性别”和“治疗方法”）。

　　3. 设置模型

　　接下来，你需要设置模型选项，以便获得更为详细的分析结果。在GLM分析对话框中，你可以进行以下设置：

　　1. 选择交互作用

　　确保在“固定因子”框中的两个自变量之间选择交互作用项。SPSS会自动计算两个自变量的主效应以及它们的交互效应。交互作用是指自变量之间的联合效应，即它们一起作用时对因变量的影响是否不同于它们分别作用时的效应。

　　2. 检验方差齐性

　　方差齐性检验（如Levene检验）是双因子方差分析中的一项重要步骤。在SPSS中，你可以通过选择“选项”按钮，勾选“方差齐性检验”来确保数据符合方差齐性假设。

　　3. 选择事后检验

　　如果双因子方差分析结果显著，你可能希望进一步了解哪些组之间存在显著差异。在SPSS中，你可以选择进行事后检验（如Tukey、Bonferroni等），这将帮助你识别组间差异。

　　4. 执行分析并查看结果

　　点击“确定”后，SPSS会执行双因子方差分析，并生成以下输出：

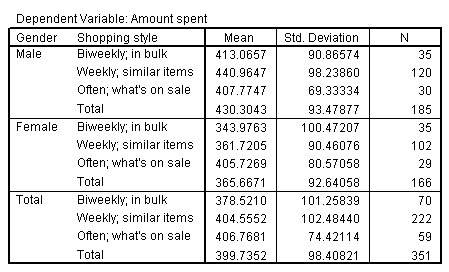
　　描述性统计表：显示每个组的均值、标准差等统计量。方差分析表（ANOVA表）：提供各因变量主效应、交互效应的F值、p值等重要统计结果。通过查看这些结果，你可以判断自变量对因变量的主效应是否显著，以及交互效应是否显著。事后检验结果：如果方差分析表中的结果显著，SPSS还会根据你选择的事后检验方法，给出哪些组之间差异显著的详细信息。

　　5. 解读结果

　　1. 主效应

　　主效应是指每个自变量对因变量的独立影响。例如，你可以查看“性别”和“治疗方法”对“成绩”的影响是否显著。如果p值小于0.05，则表示该自变量对因变量有显著影响。

　　2. 交互作用效应

　　交互作用效应表示两个自变量联合作用对因变量的影响。如果交互作用显著（p值小于0.05），说明自变量之间的联合效应对因变量有影响。此时，你需要进一步分析交互作用的性质，可以通过绘制交互作用图来帮助理解。

　　3. 事后检验

　　如果方差分析结果显著，SPSS会进行事后检验，帮助你识别哪些组之间的差异显著。例如，如果“性别”和“治疗方法”的交互效应显著，事后检验将帮助你确定哪些性别和治疗方法的组合对成绩有不同的影响。

　　6. 总结与应用

　　通过GLM单变量分析，SPSS可以有效地执行双因子方差分析，帮助你研究多个自变量对因变量的独立效应和交互效应。这种方法广泛应用于各种领域，如医学研究、教育评估、市场分析等。掌握GLM单变量分析的技巧，能够让你更深入地理解数据之间的关系，并为决策提供科学依据。

　　小贴士

　　在使用双因子方差分析时，确保数据符合方差齐性假设。若不符合，可能需要使用其他方法进行调整，如数据变换或使用非参数检验。若数据存在交互作用效应，建议绘制交互作用图，这有助于直观地理解不同自变量组合的影响。在分析过程中，注意对事后检验结果的解读，以便获得更加精确的结论。